平差系统验后单位权中误差最优值的估算
一、引言 验后单位权中误差是测量平差系统外业观测成果评定的重要指标。文献[1-4]研究经典测量平差数学模型及其内在几何联系，总结附加约束条件的参数平差模型为测量平差概括模型，并给出验后单位权中误差的估算公式。文献[5-8]研究验后单位权中误差与起...
- 作者：谢波来源：重庆水利电力职业技术学院|2014年12月26日
一、引言
验后单位权中误差是测量平差系统外业观测成果评定的重要指标。文献[1-4]研究经典测量平差数学模型及其内在几何联系，总结附加约束条件的参数平差模型为测量平差概括模型，并给出验后单位权中误差的估算公式。文献[5-8]研究验后单位权中误差与起算数据误差、先验单位权中误差、观测值定权方式等因素的相互关系，并应用于精度评定、粗差探测等方面。
合理选择或增加先验约束能够改善解的质量[9-10]和使验后单位权中误差产生增益[11-13]。文献[11]从随机模型误差和函数模型误差两个方面，推导附加约束条件对平差结果的影响，并以平差后的验后单位权中误差减小为条件，分析附加额外约束产生精度增益的条件。文献[12]将附有参数先验精度信息的平差问题扩展为参数约束平差，在数值上统一为自由网平差和附合网平差，得出一旦观测网形和观测方案确定，验后单位权方差是惟一的结论。文献[13]采用顾及先验信息的贝叶斯估计方法，通过设计虚拟观测值，推导顾及先验信息的平差函数模型和最优参数估计公式，得到先验精度和虚拟观测值的质量与平差精度之间的关系及单位权方差的计算式。
随着认识的深入，大地测量学者将经典测量平差概括模型扩展为附加不等式约束的测量平差统一模型，运用概率统计[14]、贝叶斯估计[15]、凝聚约束法[16-17]、线性互补法[18]、拉格朗日乘子迭代法[19]、构建虚拟误差方程[20-21]等方法来研究不等式约束对平差结果的影响和求解待估的参数，并给出各种形式不同的验后单位权中误差估算公式[16-21]。其中，附加不等式约束的测量平差统一模型在解算验后单位权中误差时，需将不等式约束转化为具有等式形式的有效约束[22]。
本文研究验后单位权中误差时，采用附加等式约束的测量平差概括模型为基础，根据附加等式约束线性模型参数估计的平差过程，利用正定二次型矩阵极值的方法进一步分析等式约束对平差结果的影响，提出附加等式约束平差系统的验后单位权中误差有两个确定的理论上的极值，推导出附加等式约束平差系统的验后单位权中误差最小值和平差系统验后单位权中误差最优值的计算公式。最后以一个水准网平差的例子验证了上述结论的正确性。
二、验后单位权中误差的计算
测量平差概括模型可以描述为[1-4]
(1)
(2)
其中（1）式为观测方程，（2）式为约束方程，L为n×1观测向量，n为观测向量的个数，B为n×u观测方程系数矩阵，X为u×1未知参数向量，u为未知参数向量的个数，C为s×u约束方程系数矩阵，
为s×1约束向量，s为约束条件个数，V为n×1改正数向量，具有0均值与方差-协方差阵
，
是协因数矩阵，
是权矩阵。
当无约束条件时，参数估计
(3)
单位权方差估值
(4)
式中
表示无约束条件时的残差的二次型，
为自由度。
当附加约束条件时，参数估计
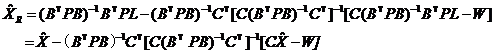(5)
残差的二次型[15]
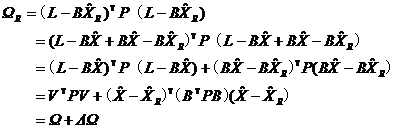(6)
式中
表示引入等式约束条件造成的残差二次型的变化。
(7)
单位权方差估值
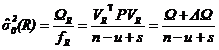(8)
要使附加约束条件后的精度提高，此时应满足以下条件：
（9）
即
（10）
附约束条件时的残差的二次型
由两项组成，第一项
是不受约束条件影响的，仅考虑第二项
。
根据二次型矩阵的性质[23-24]：对 
是
的特征根，则
。
分析二次型
，假设
是对称方阵
的最小特征根，则
存在极小值
(11)
相应的单位权方差有极小值
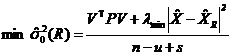(12)
由于权阵
为对称正定矩阵，所以
也是正定矩阵。根据正定矩阵的所有特征根都是正数的性质[25]，矩阵
的特征根
。所以，当且仅当
时，即：无约束条件的观测方程的参数估计
满足约束条件方程
(13a)
即
(13b)
附加约束条件线性模型的验后单位权中误差可以取得最小值
(14)
上式和一般的测量平差概括模型的单位权中误差计算公式的区别在于
为无附加约束条件时的残差，
为无附加约束条件时未知参数的个数。
三、平差系统验后单位权中误差最优值的估算
约束条件可以看做仅有必要起算数据的平差系统所增加的限制条件。在建立附加约束条件平差模型中的观测方程时，可以假设平差系统仅有必要起算数据，选取必要观测值的个数为未知参数的个数
。当约束条件的个数
取得最大值
时，平差系统验后单位权中误差将取得最优值。
下面分不同类型的平差问题来讨论。
1．水准网
假设水准网的观测值的个数为
，水准网中点的个数为
个。水准网的必要起算点的个数为1个，不考虑其他已知点，则必要观测值的个数
=
-1，约束条件的个数
可以取得最大值
=
-2，从而得到平差系统单位权中误差最优值的估值
(15)
2．二维网[1]
（1）测角网
假设测角网的观测值的个数为
，测角网网中已知点的个数为
，未知点的个数为
，测角网的必要起算点的个数为2，不考虑其他已知点，则必要观测值的个数
=2(
+
-2)，约束条件的个数
可以取得最大值
=2(
+
-3)。上式要求
+
≥3，即测角网点的总个数不小于3。从而得到平差系统单位权中误差最优值的估值
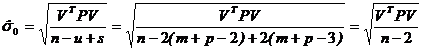(16a)
（2）测边网和边角网
假设测边网或边角网的观测值的个数为
，测边网或边角网中已知点的个数为
，未知点的个数为
，测边网或边角网的必要起算点的个数为1，以及必要起算方位角个数为1，不考虑其他已知点，则必要观测值的个数
=2(
+
-2)+1=
=2(
+
-1.5)，约束条件的个数
可以取得最大值
=2(
+
-3)+1=2(
+
-2.5)。上式要求
+
≥3，即测边网或边角网点的总个数不小于3。从而得到平差系统单位权中误差最优值的估值
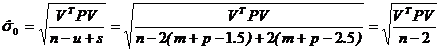(16b)
3．三维(GPS)网[26]
假设三维网的观测值的个数为
，三维网中已知点的个数为
，未知点的个数为
，三维网的必要起算点的个数为1，不考虑其他已知点，则必要观测值的个数
=3(
+
-1)，约束条件的个数
可以取得最大值
=3(
+
-2)。上式要求
+
≥3，即三维网点的总个数不小于3个。从而得到平差系统单位权中误差最优值的估值
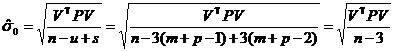(17)
上述计算公式中的
均为平差系统仅有必要起算数据，未知参数的个数
取为必要观测值的个数
时来建立的平差模型的残差值。
四、算例
以水准网为例证明上述结论。
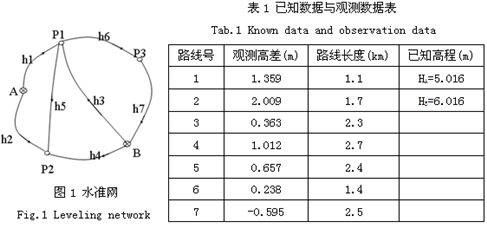
如图1，
是已知的高程点，
是待定点。已知数据与观测数据列于表1。求各点的高程平差值。
设
、
点的高程为
，未知参数
=4，观测数
=7，必要观测数
=3，多余观测数
=7-3=4。按距离定权，取
=1。取相应的近似值
，
，
，
，则
，
，，
，
，未知参数为
。
列误差方程：
约束条件方程：
(18)
式中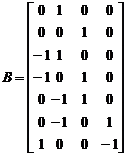
，
。
计算与分析：
1)已知起算数据为
，经平差计算得到无约束条件时的单位权中误差为 2.34mm，
=16.43mm2。
2)在约束条件为式(18)时，约束方程系数C为1×4矩阵，C= [1 0 0 0]；约束向量WX为1×1矩阵，
WX=C (BTPB)-1BTPL= [-2.410] mm.
附加一个约束条件的验后单位权中误差的最小值为
上述结果可以从图2的数值模拟得到验证。通过对B点的高程HB=6.016m施加偏差，验后单位权中误差的变化曲线中存在极小值2.03mm，和公式计算结果一致。
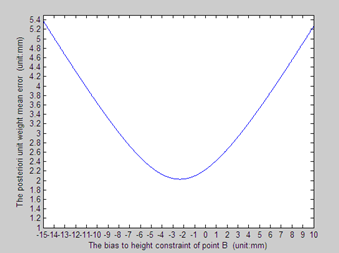
图2 验后单位权中误差和点B高程偏差的变化图
3)增加约束条件的个数，假设点
也为已知，则增加的约束条件为
(19)
约束方程系数C为2×4矩阵，C=[1 0 0 0;0 1 0 0]；约束向量WX为2×1矩阵，WX= C (BTPB)-1BTPL = [-2.410; -1.326] mm.
附加二个约束条件的验后单位权中误差的最小值为
数值模拟结果如图3所示，验后单位权中误差的的极小值1.81mm，数值模拟结果和公式计算结果一致。
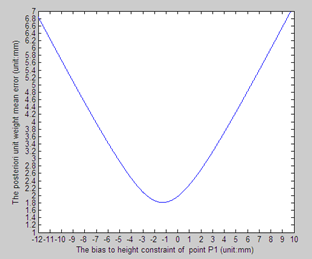
图2 验后单位权中误差和点P1高程偏差的变化图
4)增加约束条件的个数，假设点
也为已知，则增加的约束条件为
(20)
约束方程系数C为3×4矩阵，C= [1 0 0 0;0 1 0 0;0 0 1 0]；约束向量WX为3×1矩阵，WX= C (BTPB)-1BTPL =[-2.410;-1.326; 1.878].
附加三个约束条件的验后单位权中误差的最小值为
数值模拟结果如图4所示，验后单位权中误差的的极小值1.66mm，数值模拟结果和公式计算结果一致。
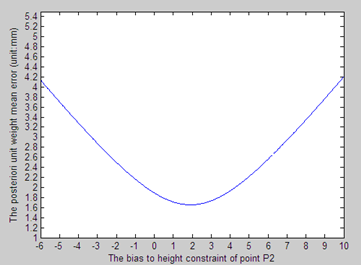
图4 验后单位权中误差和点P2高程偏差的变化图
该值也是该平差系统验后单位权中误差最优值。运用公式（15）计算水准网平差系统验后单位权中误差最优值为
两者结果一致。
五、结束语
1) 通过设计或改变约束条件方程的约束向量，总可以使得附约束条件线性模型的验后单位权中误差的估值取得最小值，该最小值由无附加约束条件的观测方程的形式、观测值的个数和约束条件的个数确定。
2）增加约束条件个数可以提高精度，而实际上先验约束都有一定的误差。应用本文的附加约束条件下单位权中误差最小值公式可以判断先验约束的合理性，或选择先验约束的个数，从而方便和优化测量基准设计。
3)对于任意一个现实中具体的平差系统，该系统的网形和观测值确定以后，则在理论上该平差系统验后单位权中误差最优值是唯一存在的，该值由仅有必要起算数据的观测方程和观测值的个数确定，且和必要起算数据的选取无关。
4)平差系统验后单位权中误差最优值是平差系统验后单位权中误差的最小值，是测量平差系统的验后单位权中误差的“先验值”，在没有验前统计信息时，可以将其作为限差的基准值以及方差一致性检验的验前值。
参考文献：
[1] 於宗俦,于正林.测量平差原理[M].武汉测绘科技大学出版社,1990.127-130.
[2] 王新洲.论经典测量平差模型的内在联系[J].测绘通报,2004(2): 1-4.
[3] 赵超英,张勤.再论经典测量平差模型间的内在联系[J].测绘通报,2006(3): 26-27.
[4] 康壮,隋立芬.论经典平差模型的几何统一[J].测绘科学技术学报,2006,23(4):290-292.
[5] 黄加纳.顾及起始数据误差影响时单位权中误差的估值[J].武汉测绘科技大学学报,1986,26(4):64-73.
[6] 曾宪珪,李满苗.精度评定中合理顾及起算数据误差之研究[J].南方冶金学院学报,1993,14(4):273-281.
[7] 吕伟才.先验单位权中误差对平差成果的影响[J].勘察科学技术,1999(1):51-54.
[8] 王磊,郭际明,喻永平,申丽丽.水准网定权方法对精度评定的影响[J].测绘通报,2011(5):26-28.
[9] 欧吉坤.测量平差中不适定问题解的统一表达与选权拟合法[J].测绘学报,2004,33(4): 283-288.
[10] 欧吉坤,王振杰.单频GPS快速定位中模糊度解算的一种新方法[J].科学通报,2003,48(24):2572-2575.
[11] 姚宜斌.GPS精密定位定轨后处理算法与实现[D].武汉大学,2004,24-30.
[12] 刘根友,郝晓光,柳林涛.参数约束平差法[J].大地测量与地球动力学,2006,26(4):5-9.
[13] 邓兴升,陈石桥,丁美青.顾及先验信息的变形监测网平差[J].大地测量与地球动力学, 2013,33(2):45-48.
[14] 朱建军,谢建,陈宇波.不等式约束对平差结果的影响分析[J].测绘学报,2011,40(4):411-415.
[15] ZHU J, SANTERRE R, CHANG X-W. A Bayesian Method for Linear, Inequality constrained Adjustment and Its Application to GPS Positioning [J]. Journal of Geodesy, 2005, 78:528-534.
[16] PENG Junhuan, GUO chunxi, ZHANG Hongping, et al. An Aggregate Constraint Method for Inequality-Constrained Least Squares Problems [J]. Journal of Geodesy, 2006, 79(2):705-713.
[17] 彭军还,张亚莉,章红平,等.不等式约束最小二乘问题的解及其统计性质[J].测绘学报,2007,36(1):50-55.
[18] 宋迎春,左廷英,朱建军.带有线性不等式约束平差模型的算法研究[J].测绘学报,2008,37(4):433-437.
[19] 冯光财,朱建军,陈正阳,等.基于有效约束的附不等式约束平差的一种新算法[J].测绘学报,2007,36(2):119-123.
[20] 欧阳文森,朱建军.虚拟误差方程解决附不等式约束的平差问题[J].测绘通报,2007(1):20-23.
[21] 欧阳文森,朱建军.经典平差模型的扩展[J].测绘学报,2009,38(1):12-15.
[22] LU G, KARKIWSKYEJ, LACHAPELLEG. Application of Inequality Constraint Least Squares to GPS Navigation under Selective Availability [J]. Manuscripta Geodaetica, 1993, 18:124-130.
[23] 王松桂,吴密霞,贾忠贞.矩阵不等式[M].北京:科学出版社,2006. 121-128.
[24] 陈荣群,黄勇.二次型在求条件极值中的应用[J].福建教育学院学报, 2008(10):98-101.
[25] 方保镕,周继东,李医民.矩阵论基础(第二版)[M].南京:河海大学出版社,2003,108-111.
[26] 李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2005.3,245-246.
Estimation of the Posterior Optimal Value of Unit Weight Mean Error
for Adjustment System
(Construction Department of Chongqing Hydroelectric College，Chongqing，402160)
Abstract：Some priori constraints are applied on parameter in the surveying data processing. Analyze the condition of gain or loss for adjustment results from priori constraints, and use the method of extreme value of positive definite quadratic matrix to solve the minimum value and its condition of the incremental part of quadratic form of residual error, and deduce the two extreme value of the actual posteriori unit weight mean error，conclude the minimum value of unit weight mean error with additional constraints and the optimal value of posterior unit weight mean error in adjustment system. Finally a level of net adjustment example verifies the conclusion of the paper. The studies have value in the aspect of designing surveying datum and selection of priori unit weight mean error.
Keywords: Equality Constraints；Adjustment；Unite Weight Mean Square Error；Optimal Value
作者：谢波
地址：重庆水利电力职业技术学院建筑工程系
邮编：402160
手机：15870513682
作者简介：谢波（1973—），男别，汉族，湖北宜城人，硕士，讲师，工程师，主要研究方向为精密工程测量、测量数据处理。
