椭球面上绘制大地线的算法研究
1 引言 参考椭球面是最接近地球表面的可用数学方法表达的标准面,基于椭球面表达地表对象是最适合的地图表现形式。基于此,为了摆脱地图投影给大区域地理信息表达带来的种种不利影响,杨永崇等[1]介绍了椭球面电子地图的设想,该设想有效地解决了大区域或...
- 作者:唐红涛,王 微,保长燕,孙兴华,杨永崇来源:2014测绘学会|2014年12月26日
参考椭球面是最接近地球表面的可用数学方法表达的标准面,基于椭球面表达地表对象是最适合的地图表现形式。基于此,为了摆脱地图投影给大区域地理信息表达带来的种种不利影响,杨永崇等[1]介绍了椭球面电子地图的设想,该设想有效地解决了大区域或全球范围数字地图和GIS的表达问题,实现该设想需要解决的一个关键问题就是如何在椭球面上绘制大地线。大地线是椭球面上两点的最短连线,它是一条函数方程比较复杂的空间曲线。基于该性质,在涉及描述地球表面或近地空间相关学科的问题时[2-5],经常会遇到此类问题,如:为了避免参考框架对GPS计算结果的影响,采用大地线长度的时序变化来研究两站之间的相对运动;在涉及求解、构造大地线的平行线及国家间海洋精确划界问题时,如一个国家的领海基线、毗连区界线等。
借鉴平面曲线的绘制方法,可采用曲线光滑技术绘制大地线,即用一系列空间直线段逼近大地线,当大地线的长度小于某个阙值时可近似为直线段,超过某个阙值时则需要通过内插点位方式以保证其曲率和长度。因此,绘制大地线的核心问题首先是根据两点的大地坐标确定其大地线的函数,然后计算出该大地线上各加密点的大地坐标。
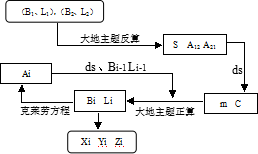
本文通过应用Bessel大地主题正、反算以及克莱劳方程给出一种实现大地线内插与绘制的综合解算方法。
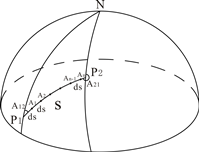
如图1(a)所示,首先由椭球面两个已知点的精确大地坐标![]() 、
、![]() 进行Bessel大地主题反算,获取大地线长
进行Bessel大地主题反算,获取大地线长![]() 、大地方位角
、大地方位角![]() 、大地反方位角
、大地反方位角![]() ;随后从
;随后从![]() 点开始,根据给定的空间等直线段
点开始,根据给定的空间等直线段![]() 、正方位角
、正方位角![]() 进行Bessel大地主题正算,求解第一个内插点的大地坐标
进行Bessel大地主题正算,求解第一个内插点的大地坐标![]() ;根据点
;根据点![]() 和克莱劳定理解算大地线常数
和克莱劳定理解算大地线常数![]() 及第1个内插点的前进方向大地方位角
及第1个内插点的前进方向大地方位角![]() ,以此推算出第二个内插点的大地坐标
,以此推算出第二个内插点的大地坐标![]() 和该点的前进方向大地方位角
和该点的前进方向大地方位角![]() ……以此循环推算大地线各内插点的大地坐标。该过程以椭球面为基准面进行解算,最后在大地线的表达中,需将各内插点的大地坐标转化为同一参考椭球下的空间大地直角坐标,利用空间直线段连接各加密点对大地线进行逼近绘制。
……以此循环推算大地线各内插点的大地坐标。该过程以椭球面为基准面进行解算,最后在大地线的表达中,需将各内插点的大地坐标转化为同一参考椭球下的空间大地直角坐标,利用空间直线段连接各加密点对大地线进行逼近绘制。
大地线的三个微分方程给出了大地线长度、大地经纬度与大地方位角之间的微分关系,而在椭球面上对该微分方程进行积分是相对困难的,需将被积函数按级数展开逐项积分,Bessel法不同于勒让德级数、高斯平均引数法的是,它将被积函数展开为椭球偏心率的幂级数,更适用于长距离大地问题解算。Bessel法解算大地主题的思想是根据大地投影的三个条件[6]将椭球面上的大地元素按照Bessel投影条件投影到辅助球面上,继而在球面上进行大地主题解算,最后再将球面上的计算结果换算到椭球面上。
|
|
|
|
(a) |
(b) |
|
图1 求解大地线内插点大地坐标及流程图 | |
通过参考椭球空间直角坐标系中椭球面法向量与以大地线弧长为参数的大地线主法线向量指向的一致性,可获得克莱劳恒等式。直角坐标系中椭球面方程(1)和椭球面法向量(2)如下:
![]() (1)
(1)
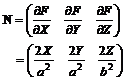 (2)
(2)
以大地线弧长为参数的大地线主法线向量:
![]() (3)
(3)
由空间直角坐标与大地坐标的微分关系:
 (4)
(4)
经整理:![]() 及
及![]() ,此式即为克莱劳方程。式中:
,此式即为克莱劳方程。式中:![]() 为大地线上点的所在纬度平行圈半径,
为大地线上点的所在纬度平行圈半径,![]() 为该点的大地线方位角,
为该点的大地线方位角,![]() 为大地线常数。克莱劳方程表明,在参考椭球上,大地线上各点的平行圈半径与大地线在该点大地方位角正弦的乘积为一个常数。基于此,首先由
为大地线常数。克莱劳方程表明,在参考椭球上,大地线上各点的平行圈半径与大地线在该点大地方位角正弦的乘积为一个常数。基于此,首先由![]() 及大地反算出的
及大地反算出的![]() 计算大地线常数
计算大地线常数![]() ,随后在大地线内插计算过程中,每点前进方向的大地方位角
,随后在大地线内插计算过程中,每点前进方向的大地方位角![]() 便可求出。
便可求出。
一条大地线的大地线常数并非唯一,即同一条大地线对应两个常数。这是由大地线正、反方位角所引起的,如图1(a)所示,从![]() 走向
走向![]() 时,大地方位角
时,大地方位角![]() 小于180度,
小于180度,![]() ;反之若取
;反之若取![]() ,则
,则![]() 。因此在实现大地线内插中,需先指明大地线方向。在特殊情况下,当大地线与子午线完全重合时,
。因此在实现大地线内插中,需先指明大地线方向。在特殊情况下,当大地线与子午线完全重合时,![]() ;当大地线与赤道完全重合时,
;当大地线与赤道完全重合时,![]() 。
。
根据上述大地线内插算法及其表达绘制的要求,选择VC++6.0作为程序测试环境,分别对如下两个算例进行了解算。
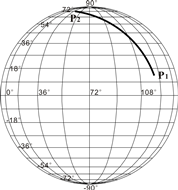
算例一、算例二给出了数据解算结果与大地线绘制图,计算过程是在1975国际参考椭球面上进行的,解算结果包括由已知点反算的大地方位角A12、反方位角A21、大地线长S、大地线每个内插点前进方向(大地线绘制方向,本文均采用P1至P2方向)的大地方位角Ai及大地坐标(Bi,Li)。大地线在椭球面上绘制表达中使用空间直角坐标较为方便,所以还需将每个内插点的大地坐标转换为同一系统下的空间大地直角坐标(Xi,Yi,Zi)。此外,椭球定向的详细过程见文献[7-11],大地线上采用等间距(ds)内插,取ds为10km,解算结果见表1、表2,绘制图如图2所示。
算例一,正方位角A12为 340°26′49.712929″,大地线长S为8233.744892 km,内插点823个,各点的大地方位角在第四象限随纬度的增加而减小,减小的幅度却逐渐变大。
算例二,正方位角A12为25°20′44.600932″,大地线长S为12561.938626 km,内插点1256个。从表2中可知,南半球各内插点的大地方位角随着P1点向赤道圈的前进在变小,而平行圈半径趋大,389号点离赤道圈最近(其空间大地直角坐标中Z的绝对值最小),390号点刚过赤道圈,大地方位角Ai继而开始转为增加,平行圈半径开始减小。
|
|
|
|
(a)算例一 |
(b) 算例二 |
|
图2 大地线绘制图 | |
表1 算例一解算结果
|
序号 |
大地方位角 Ai |
大地坐标 |
空间大地直角坐标 | |||
|
Bi |
Li |
Xi /m |
Yi /m |
Zi /m | ||
|
1 |
340°26′25.056757″ |
12°52′30.098092″ |
120°26′30.690573″ |
-3150838.7330 |
5361520.6672 |
1411929.8029 |
|
2 |
340°26′00.224429″ |
12°57′36.722912″ |
120°24′39.608573″ |
-3146884.6033 |
5361400.1066 |
1421114.0655 |
|
3 |
340°25′35.214184″ |
13°02′43.332567″ |
120°22′48.451027″ |
-3142922.6966 |
5361266.2963 |
1430294.7925 |
|
4 |
340°25′10.025739″ |
13°07′49.926945″ |
120°20′57.217371″ |
-3138953.0227 |
5361119.2367 |
1439471.9611 |
|
5 |
340°24′44.658809″ |
13°12′56.505937″ |
120°19′05.907043″ |
-3134975.5916 |
5360958.9284 |
1448645.5484 |
|
… |
… |
… |
… |
… |
… |
… |
|
822 |
277°18′08.386717″ |
70°50′44.200281″ |
42°45′45.319580″ |
1541065.9172 |
1425172.7297 |
6002652.0633 |
|
823 |
277°02′47.106004″ |
70°51′24.495757″ |
42°29′30.078467″ |
1546917.1019 |
1417073.6139 |
6003061.7163 |
|
采用1975国际椭球参数 P1(B1,L1):(12°47′23.458231″,120°28′21.697512″) a =6378140.0 m P2(B2,L2):(70°51′39.224785″,42°23′24.286583″) e2 =0.006694384999588 S= 8233744.891615 m A12= 340°26′49.712929″ A21= 96°57′00.933717″ | ||||||
表2:算例二解算结果
|
序号 |
大地方位角 Ai |
大地坐标 |
空间大地直角坐标 | |||
|
Bi |
Li |
Xi /m |
Yi /m |
Zi /m | ||
|
1 |
25°19′16.732851″ |
-32°23′59.912931″ |
40°39′10.699292″ |
4089554.4681 |
3511731.0962 |
-3397961.6779 |
|
2 |
25°17′49.218117″ |
-32°19′06.436974″ |
40°41′54.209317″ |
4090437.6953 |
3518126.9308 |
-3390325.4005 |
|
3 |
25°16′22.056324″ |
-32°14′12.898484″ |
40°44′37.426630″ |
4091310.8473 |
3524514.0998 |
-3382680.7161 |
|
… |
… |
… |
… |
… |
… |
… |
|
388 |
21°11′24.140536″ |
-0°06′14.681289″ |
54°45′50.915418″ |
3679825.6273 |
5209550.8326 |
-11508.3528 |
|
389 |
21°11′24.014213″ |
-0°01′11.121132″ |
54°47′47.809950″ |
3676878.4876 |
5211643.6604 |
-2184.4899 |
|
390 |
21°11′24.059924″ |
0°03′52.439054″ |
54°49′44.704366″ |
3673922.2566 |
5213723.6020 |
7139.3785 |
|
391 |
21°11′24.277669″ |
0°08′55.999159″ |
54°51′41.599169″ |
3670956.9415 |
5215790.6523 |
16463.2293 |
|
… |
… |
… |
… |
… |
… |
… |
|
1255 |
61°40′23.891675″ |
65°49′38.865160″ |
114°07′07.524094″ |
-1070224.5066 |
2390429.0934 |
5796095.7890 |
|
1256 |
61°50′57.499967″ |
65°52′11.622769″ |
114°18′41.913780″ |
-1076488.3642 |
2382878.2022 |
5798031.6616 |
|
采用1975国际椭球参数 P1(B1,L1):(-32°28′53.326356″,40°36′26.895231″) a =6378140.0 m P2(B2,L2):(65°52′41.215863″,114°20′57.9158742″) e2 =0.006694384999588 S= 12561938.626520 m A12= 25°20′44.600932″ A21= 241°53′02.151660″ | ||||||
从上述两个算例可以获知,大地线各内插点方位角的变化幅度在赤道圈处较小,越靠近两极其变化量越大;同时,在内插点大地方位角Ai和其平行圈半径的动态变化中,始终遵循克莱劳定理,这在大地问题解算以及将来椭球面数字地图的相关量算、绘制等分析与编辑的算法实现中,都具有极其重要的作用。
大地线是椭球面上两点间的最短连线,它是一条函数方程较为复杂的空间曲面曲线。在对大地线进行表达时,本文采取了用空间直线段对其逼近的形式。在算例中,由程序完成已知点间的Bessel大地反算、结合克莱劳方程与大地正算迭代计算各内插点大地坐标、以及由大地坐标向空间直角坐标转换的具体解算过程,并形成了大地线绘制图。
随着三维GIS技术的发展和推广,在表达大区域地理要素时,将会采用椭球面来表达空间数据,而大地线作为椭球面上的基本线元,在点、线、面、体四大类空间实体的表达中将会起到重要的作用。
[1] 杨永崇,竟 霞.基于椭球面大尺度表达地表对象方法研究[J].测绘通报,2011(12):22-25
[2] 田德森.现代地图学理论[M].北京:测绘出版社,1991
[3] 杨永崇,郭达志.基于地理坐标的数字地图量算模型[J].西南交通大学学报,2005.40(3):318-321
[4] 马荣华,黄杏元.GIS认知与数据组织研究初步[J]. 武汉大学学报·信息科学版,2005,30(6):539-543
[5] 纪 兵,边少锋.大地主题问题的非迭代新解[J].测绘学报,2007,36(3):269-273
[6] 孔祥元,梅是义.控制测量学[M].武汉:武汉大学出版社,2002.
[7] 史国友,周晓明,贾传荧.贝塞尔大地主题正解的改进算法[J].大连海事大学学报,2008,34(1).
[8] 孔祥元,郭际明,刘宗泉.大地测量学基础(下册)[M].武汉:武汉大学出版社,2010.
[9] 冯 琰,施一民.基于区域性椭球面数字地面模型的研究[J].同济大学学报(自然科学版),2003,31(8).
[10] 廖 克.现代地图学的最新进展与新世纪的展望[J].测绘科学,2004,29(1).
[11] 施一民.现代大地控制测量[M].北京:测绘出版社,2003.
Study on algorithm of expressing geodesic on ellipsoid surface
TANG Hong-tao1, WANG Wei2, BAO Chang-yan3, SUN Xing-hua4,YANG Yong-chong5
(1. Second Crust Monitoring and Application Center,CEA,Xi’an 710054,China;2. Tianjin StarGIS Information Engineering CO.,LTD,Tianjin 300384,China;3. 2nd Institute of Surveying & Mapping Qinghai Province, Xining 810001,China;4. Shanxi Provincial Transport Planning Design and Research Institute,Xi’an 710035,China;5. Department of Surveying engineering Xi'an University of Science and Technology,Xi’an 710054,China)
Abstract: Is the standard reference ellipsoid surface closest to the Earth's surface can be used mathematical methods of expression, the expression of surface objects based on the ellipsoid is the most suitable form of maps. Geodesic is the basic line segment on ellipsoid surface, in order to express regional geographical element on ellipsoid surface accurately, it need to be studied on algorithm for mapping geodesic. This paper applied idea for approximating spatial curve with spatial straight line, gave a method for actualizing geodesic interpolation and expressing with Bessel geodetic problem solution and Clairaut's theorem, and verified the correctness of the method with two examples.
Key words: Geodetic surveying technology; Ellipsoid surface digital / Electronic map; Geodesic; Clairaut's Theorem; Bessel Geodetic Solutio
上一篇:天文经度测量中人仪差改正精度分析