CASS软件中方格网法计算土方量的原理及误差分析
1 绪论 1.1概述 在各种工程建设如铁路、公路、港口、城市规划等中,土方量计算是一项经常性的、不可缺少的工作,且在整个工程量中,土方工程常占有较大比例。土方量计算精度的高低直接影响到建设工期、经济效益。需要合理的进行土方调配,节省施工费用,...
- 作者:罗 林来源:2014测绘学|2015年01月04日
1 绪论
1.1概述
在各种工程建设如铁路、公路、港口、城市规划等中,土方量计算是一项经常性的、不可缺少的工作,且在整个工程量中,土方工程常占有较大比例。土方量计算精度的高低直接影响到建设工期、经济效益。需要合理的进行土方调配,节省施工费用,加快工程进度。因此,研究土方量的计算方法,精度及计算方法的实用范围、条件和存在的问题是非常必要的[1]。
土石方工程量的计算,实际上就是计算设计标高与自然地面标高之间的土石方体积。设计面有平面、斜面、曲面,而自然地面更是变化多端,要求计算出来的工程量绝对准确,一般来说不大可能,也不必要,因为要精确计算土石量,则对地形测量的资料要求非常高,这样会大大增加土石方量的成本。
1.2国内外研究现状
土石方量测量与计算是测量人员的一个重要任务,也是工程预决算的基础资料,土石方量计算的正确、及时性是能否有效地进行工程建设和管理的一个重要因素。一直以来,工程技术人员计算土石方量、采石场储量通常采用方格纸用图解法来计算,这种方法精度差,速度慢,其准确性难以保证,计算的土石方量与工程施工实际土石方量往往相差达30%以上,给工程施工及造价造成极大的不确定性。因此有必要就方格网法为例对土方量计算方法及影响其准确度的因素进行探讨。
随着数字测图技术的发展,CASS软件已经得到广泛的应用,它不但有地形、地籍成图功能,也有工程应用功能,这使得土石方量计算变得快捷而准确。
1.3 本文探讨的主要问题
本文探讨的重点是利用CASS7.1平台中土石方计算的方格网法进行误差对比分析,从计算原理入手,并结合实例,通过对比分析得出结论。最终达到学习,研究,探讨的目的。为以后遇到类似问题提供理论和实践依据。
2 方格网法土石方计算的原理
2.1方格网法
该方法首先将场地划分为若干方格(一般为边长10~20m的正方形),从地形图或实测得到每个方格角点的自然标高,由给出的地面设计标高,根据各点的设计标高与自然标高之差,求出零线位置,进而求出各方格的工程量,所有方格的工程量之和即为整个场地的工程量。
方格网法计算公式很多,用不同的计算公式,工作方案和程序便不一样。一般用水准测量或三角高程测量方法,测出方格网点的标高,计算方格网的平均标高H及面积S,平均标高H可按下述几种方法计算:
1、算术平均法。将格网的四个角点高程相加求和,除以点的总数即为平均标高。
2、加权平均法。如果将每个方格的4个角点高程取平均即得该方格的平均高程。各方格的平均高程加在一起,除以方格数,即为该方格网的加权平均高程。如图2.1所示,整个区域四个角A,B,C,D的高程在计算中只用了1次,边上各点的高程用了2次,而网格内各点的高程都用了4次。各网点在计算平均高程使用时的次数即为该点的权。加权平均高程等于各网点的权乘以该点的高程的总和,除以各点权的总和[6]:
![]() (2-1)
(2-1)
式中:H平均为各方格网点的加权平均值;Hi为各方格网点高程;Pi为各方格网点的权;n为方格网点的个数。
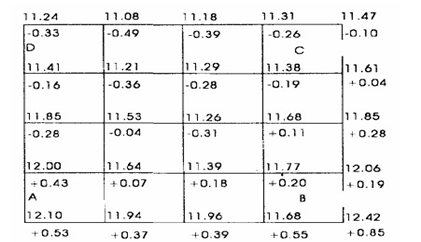
图1 格网点数据
实际作业时,计算填挖方量平衡的设计高程的计算式为:
![]() (2-2)
(2-2)
式中N为方格总数。
根据上式求得设计高程,在地形图中按内插法绘出设计高程的等高线,这条等高线就是填挖的分界线,又称零线。然后计算各方格顶点的填充高度(即施工高度)及土方量。
用方格网法计算土方量,设计面可以是水平的,也可以是倾斜的。也可以设计多个坡度[7]。
1、只有一个设计高程和设计坡度时,直接用CASS7.1软件中的“工程应用”菜单下的“方格网法土方计算”,根据提示输入相关数据即可求得土石方量。
2、有两个以上设计坡度时,假定一个设计高程H,H应比所有设计高程和原地貌高程均高或均低。
(1)零点线的确定
①根据不同设计坡度的变化计算出特征点的设计高程,特征点尽量多取一些,以便更好地控制各点的设计坡度,然后以这些特征点生成1个坐标文件:“基准面.dat”利用CASS7.1软件中的“工程应用”菜单下的“方格网法土方计算”,生成各网格点的高程,即为各点的设计高程。
②利用“原地貌.dat”坐标文件,取相同的计算边界(使生成的格网和前面生成的格网一致)生成各网格点的高程,即为各点的原地貌高程。
③将生成的两网格套在一起,根据各网格点的设计高程和原地貌高程,绘制出零点线。零点线将土方计算范围分成多个挖、填方区域。
(2)计算土石方量
①用“基准面.dat”文件按“1、”法,计算出各个挖方区域相对假定设计高程H的方量W1-1、W2-1、W3-1、……Wi-1,i表示挖方区域的个数,同理用“原地貌.dat”文件计算出相对于假定设计高H的各挖方区域的方量W1-2、W2-2、W3-2、……Wi-2,i表示挖方区域的个数。
②各挖方区域的挖方量为: W1=│W1-1- W1-2│, W2=│W2-1- W2-2│、W3=│W3-1- W3-2│……Wi=│Wi-1- Wi-2│,则全区挖方量W挖= W1+ W2+……+ Wi。
3 CASS7.1软件中土方量计算方法
由方格网来计算土方量是根据实地测定的地面点坐标(X,Y,Z)和设计高程,通过生成方格网来计算每一个长方体的填挖方量,最后累计得到指定范围内填方和挖方的土方量,并绘出填挖方分界线。
系统首先将方格的四个角上的高程相加(如果角上没有高程点,通过周围高程点内插得出其高程),取平均值与设计高程相减。然后通过指定的方格边长得到每个方格的面积,再用长方体的体积计算公式得到填挖方量。因此,用这种方法算出来的土石方量与用其它方法得出的结果会有较大的差异,一般说来,这种方法得出的结果精度不太高,这是由于这种方法“先天不足”—— 算法的局限性,但是方格网法简便直观,加上土方的计算本身对精度要求不是很高,因此这一方法在实际工作中还是非常实用的。
4 土方量计算方法的误差分析
4.1 方格网法土方量误差公式
1、公式中符号之说明
N———小方格总数;
S———小方格之边长(m);
h均———场地平均施工高度,h均=∑ph/∑p(m);
hi———小方格顶点之施工高度(m);
Pi———小方格顶点施工高度的权,∑P=4N;
mL———方格网边长之量测中误差(m);
md———内插方格网顶点高程时图上长度量测中误差(m);
mh———施工高度中误差(m);
A———场平总面积(m);
m0———等高线高程中误差(m);
h0———地形图等高距(m);
L———方格网边长(m);
V———挖(填)土石方总量(m3);
mv———土石方总量的中误差(m3);
HB,HC———位于等高线上点的高程(m);
d1,d2———内插方格网顶点的高程时,内插点分别至相邻两条等高线的垂直距离(mm);
d———内插点的高程时,过内插点与相邻两条等高线正交的图上线段长度(mm);
2、土方计算精度公式
土方计算的基本公式:
![]() (4-1)
(4-1)
对上式微积分得:
![]() (4-2)
(4-2)
对上式应用误差传播定律得:
![]() (4-3)
(4-3)
从简化问题的角度出发,设整个方格网为正方形,因此,A=L2,应用误差传播定律可得mA= 2LmL。当整个方格网中无拐点时, ![]() 。从而,
。从而,![]() ,将此结果代入(4—2)式,并进一步整理得:
,将此结果代入(4—2)式,并进一步整理得:
![]() (4-4)
(4-4)
则土方计算的相对中误差为:
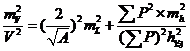 (4-5)
(4-5)
由于整个方格网无拐点,所以:
![]() (4-6)
(4-6)
将(式4-5)带入(式4-6)得:
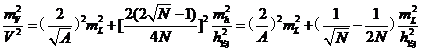 (4-7)
(4-7)
3、方格网总长测量中误差
由于人眼极限分辨率的影响,图上直线长量测中误差一般为±0.1mm,对应于实地边长量测中误差应随比例尺而定。当比例尺为1∶500时,mL=±0.05m,1∶1000时,mL=±0.10m;1∶2000时,mL=±0.20m。
4.2 方格网法土方量计算中的技巧
下面以南方CASS7.1为例,探讨方格网土方计算中的几点技巧。
1、加密高程点以提高精度
一般在测地形图时,主要考虑的是地物及绘制地形,高程点数量有限,一般难以满足土方计算对于地形图的要求。采用测绘软件来计算时,尽管电脑可以精密内插高程点,但由于电脑内插高程点时纯粹是根据定比分点原理,不能灵活参照地形,因此有时误差较大,比如对沟、坎、塘等高程较多突变的地形,电脑就无法灵活处理,如果不加以人工干预,必然会造成精度不高的结果。在计算前,除对一般的地形适当加密高程点,应重点加密沟、坎、塘、独立土堆等地方,一般要求参照地形及实测高程点在沟、坎及塘基等的上、下加密高程点。
2、设计面为斜面时要选准基准线
基准线是指斜面设计中事先确定高程完全相同的两点间连线,不难知道,当基准线和斜率确定后,该场地土地平整后的形状就确定了。也就是说,场地需填、挖方量就确定了。因此,当斜率确定时,只有精确选择好基准线,才能准确计算填、挖方量。
5 算例分析
本文以2008年绵阳市晶蓝尚城土方测算为例,通过分区域进行几种土方计算进行对比分析。全图分为A,B,C,D,E,F 6个不同设计高程区域。各个区域的设计标高为:A:473m , B:489m, C:471m ,D:478m , E:488m, F:为道路面,设计标高有多个。设计图如下所示:
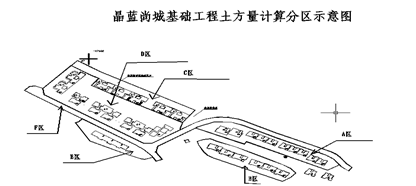
图2 晶蓝尚城设计面
由于设计面比较复杂,所以,本文拟采用分区形式计算,最后通过累计相加的方式进行计算。
土石方计算步骤:
对动土前的数字化地形图进行高程点加密。由于实测过程中有些点位未打到高程点,所以必须对原有地形的高程进行处理。这一步的主要工作是在大块的平地中按照地形情况内插入高程点,特别是在斜坡和陡坎的坎下添加高程点。这一步很重要,如果高程点密度过小,在计算土石方时,精度就相对较低。
根据设计面确定动土的边界线。通过设计面给出的区域在CASS7.1上利用“多功能复合线”功能,在设计面上确定出各个区域的动土范围。
利用CASS7.1里面的方格网法对上述6个区域进行计算土方。
统计填挖方量。将各个区域的计算值提取出来,导入到EXCEL中进行排序,然后将正的差值和负的差值分别累加起来以减少手工计算。
由于平整后A,B,C,D,E为平地,F区为复杂面,所以,在这里比较时分开讨论。由上表可以看出,如果以该方法的平均值做为土方量的最或是值,则场地比较简单时候,格网法的误差为1.2%;场地复杂时,格网法的误差为2.1%。这也正好验证了我们之前通过原理来分析误差精度的正确性。
6 结论
方格网法一般适用于地形起伏不大,且地面坡度有规律,范围比较大的施工场地,也适合平坦地区及高差不太大的地形场地平整时使用。对于中、小型建设项目、旧城区改造以及地貌复杂的情况,用方格网法计算土方量,误差较大。这样在实际工程施工中土方工程量必定与概(预)算的土方工程数量相差较大。
为提高土方计算精度和减少工作量可采取以下措施:
1、对于大面积长距离的线路工程,应根据地形状况(如起伏、宽窄、弯曲等)分成几大段,分别计算土方量,再求总和。
2、土石方计算精度确定后,测量精度和方法必须结合实际横断面的结构形状来制定,精度以需要为标准,不宜过高或过低。
3、在条件允许时,点测得密一些,特殊点和变坡点不要遗漏,尽可能缩小误差。
[1] 罗德仁,邹自力,汤江龙.工程土方量计算比较分析。东华理工学院学报.2005.3 第28卷 第1期.
[2] 柯建明,叶根生.如何规范土石方计算.学术论坛.2006.NO.33.
[3] 李志林等.数字高程模型[M].武汉:武汉大学出版社.2001.
[4] 周越轩等.基于DTM的土方工程量计算与精度分析[J].长沙交通学院学报.2000.16(4):39~43.
[5] 陈秋枫,罗德仁.横段面法土石方计算的精度分析[J].江西测绘.2003.50(3):43~44.
[6] 张正禄等.工程测量学.武汉:武汉大学出版社.2005.
[7] 杨先绪.在CASS7.1软件中多个设计坡度的土石方计算. [J].城市勘测.
[8] 林伟琦.土方量的测算及其精度分析.南方金属. [J].2001.121(5):49~52.
[9]MARTIEN Molenaar. An introduction to the theory of spatial object modeling for Taylor & Frances Press [M]. UK. 1998.
[10] WONG K W. Accuracy of Earthwork calculations from Digital Elevation Data[J]. Photogrammetric Engineering and Remote Sensing,1983,49(1).

