一种求任意多边形内部水平方向似最大矩形的算法 - 李晓晖
文章版权由作者李晓晖和博客园共有,若转载请于明显处标明出处:http://www.cnblogs.com/naaoveGIS/ 1.背景 在前一篇中,我们探讨了如何求凸多边形中的似最大圆,但是针对实际情况需求,我们并没有完全解决问题。实际情况中,凹凸多边形同时存在...
- 作者:来源:|2017年09月07日
1.背景
在前一篇中,我们探讨了如何求凸多边形中的似最大圆,但是针对实际情况需求,我们并没有完全解决问题。实际情况中,凹凸多边形同时存在,并且在行政区划应用上,凹多边形更多。所以这里我们依然得探讨如何在任意多边形中得出其内部的似最大矩形或者似最大圆。
这里,我们将方向优先选择为求似最大矩形,原因有二:矩形的判断不涉及运算,效率更高;更重要的原因是,之后我们构建R树索引,基于矩形会更加便捷。
2.算法详解
在我之前的文章《网格索引判断点面关系的方法》(http://www.cnblogs.com/naaoveGIS/p/5148185.html),提到了GIS中常用的网格方法。同样,这里我将把该网格法的思路引入至算法中。
具体描述为:
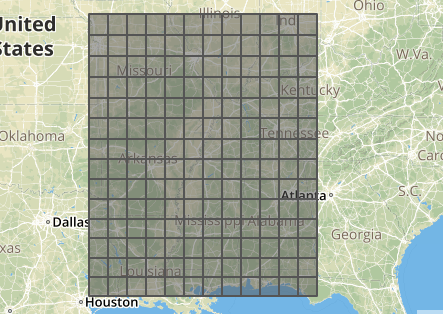
a.获取任意多边形的四角坐标,通过四角坐标构造矩形,将该矩形划分成N*M个规则格网。
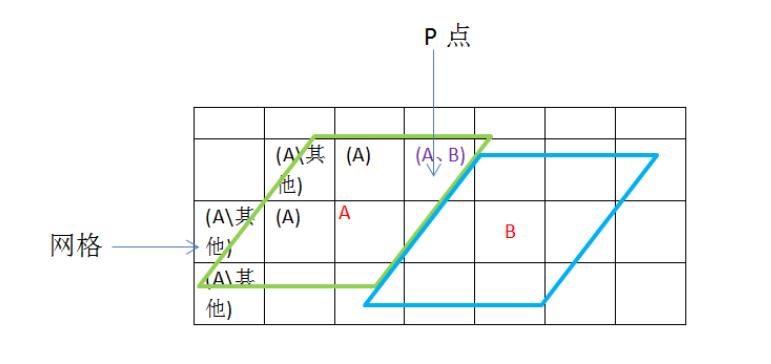
b.遍历所有格网,判断每个格网和多边形的包含关系。格网在多边形中,则标记为1,否则为0。
c.计算由0和1组成的矩形中,由1组成的最大矩形。
d.求得所得最大矩形代表的四角坐标,构造成真实地理矩形。
3.算法探讨
a.该算法最大的难点在于计算由0和1组成的矩形中,由1组成的最大矩形:

b.该算法获取的矩形是否为最大取决于网格的划分粒度,实际项目中,要进行综合考虑。实际上,只要能够逼近,是否最大不重要。
4.算法实现
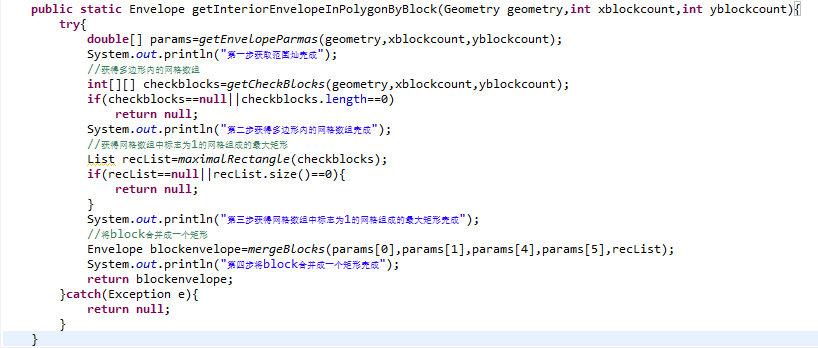
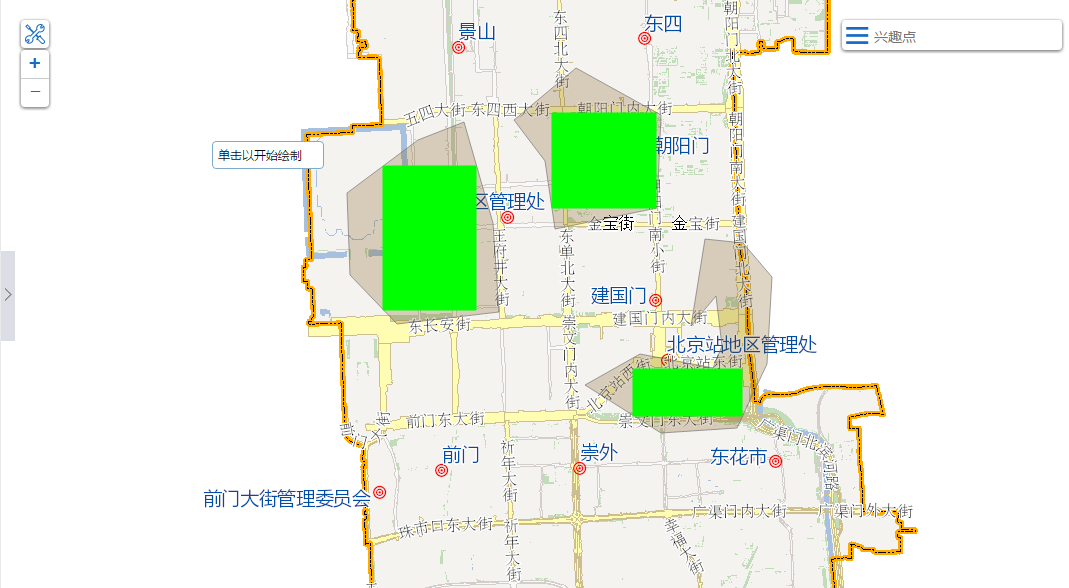
5.问题扩展
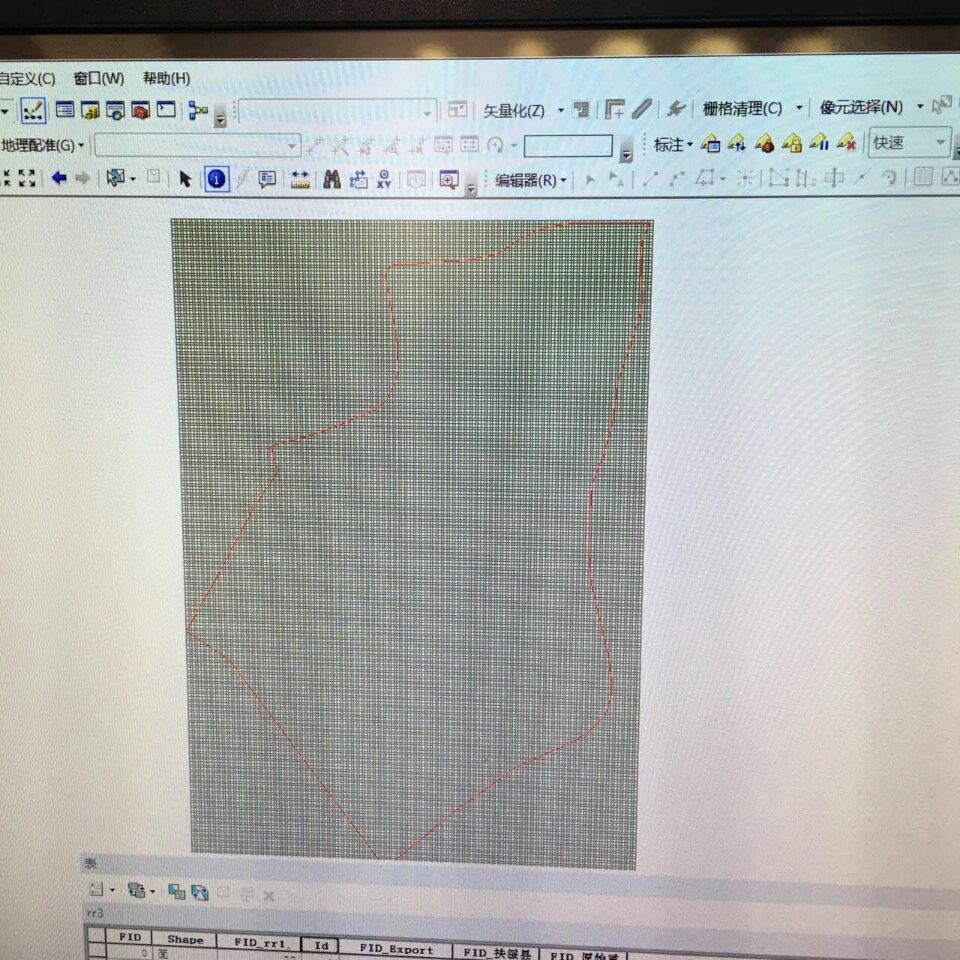
昨天一个朋友问了一个相似的问题,项目背景为土地利用分析,需要提取任意规划土地内一平方公里的样本。
利用网格的思想,该问题同样能很好的解决。
-----欢迎转载,但保留版权,请于明显处标明出处:http://www.cnblogs.com/naaoveGIS/
如果您觉得本文确实帮助了您,可以微信扫一扫,进行小额的打赏和鼓励,谢谢 ^_^


